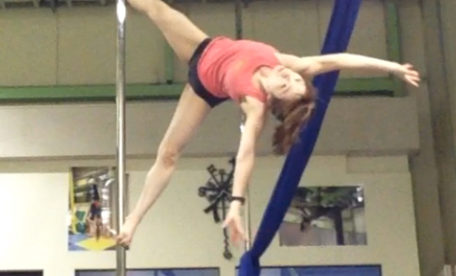(この記事はnoteで掲載しているマガジン、「理科のおさらい」を加筆修正したものです)
ーーーーーーーーーーーーーー
ポールダンスをしていて、疑問に思ったことありませんか?
「ポール自体が回転しているスピニングポールは、ポールから体を離すほど回転が遅くなる、近づくほど早くなる」
ということは体でわかる、けれどなぜ?と。
こちらの動画、最初のほうはポールの回転スピードが緩く、後半は回転スピードが上がります。
この疑問を解決すべく、中学生の理科のテキストを手に少しづつ勉強していました。
そしてようやく説明できるまでに理解できたので解説を書いてみます。
結論からいうと、フィギュアスケートのスピンと原理は同じです!
1.スピンの速さは回転軸の太さに左右される
スピンは、横幅の回転軸が
- 太ければ回転が遅く
- 細ければ回転が早くなる
回転軸が太い(細い)って何でしょうか。
ざっくり説明するために先ほどの動画を抜き出すと、下記の写真で赤線の範囲が回転軸です。細いほど回転が早くなる。
この回転軸うんぬんを物理学的に説明するために必要な概念が3つ。
「角運動量」「角速度」と「慣性モーメント」です。
まず、最初に回転運動の大きさは「角運動量(L)」という指標で表します。
角運動量(L)の求め方、つまり回転運動の大きさは、「半径(r)× 運動量(p)」
運動量(p)というのは「質量(m)と速度(v)の積で表される運動の状態」と定義されます。ざっくりいうと「勢い」と言ったところでしょうか。
ものすごーくかんたんに表すなら、「回転運動の大きさは半径 ✕ 勢い」ということになります。
つづいて、物体の運動時の考え方として「運動量保存の法則」というのがありましたが(ニュートンのゆりかご、を思い出して!)
それは回転運動の時にもあてはまります。回転運動のときは「角運動量保存則」と頭に「角」がつきます。
=角運動量保存則=
外部から摩擦などの力が加わらない場合、
角運動量(L) = 慣性モーメント(I) × 角速度(w) = 一定
つまり、角運動量(回転運動の大きさ)が一定の場合は慣性モーメントが小さくなれば角速度(回転速度)が大きくなります。
イメージしやすくするために数字を当てはめてみると
角運動量(回転運動の大きさ300)= 慣性モーメント(10)× 角速度(30)の場合に
慣性モーメントが5になると
角運動量(回転運動の大きさ300)= 慣性モーメント(5)× 角速度(60)
となります。
慣性モーメントが小さくなる=角速度が上がる(回転が早くなる)
または、角速度(回転速度)を上げるためには慣性モーメントを小さくする必要があるとも言えます。
では、慣性モーメントってなんでしょうか??
2.慣性モーメントは回転のしづらさ
慣性モーメントは、詳細な説明をすっ飛ばしてざっくりかんたんに表現するなら「回転しにくさ」のことです。「回転の始まりにくさ」「回転の止まりづらさ」。
慣性モーメントを式で表すにはちょっと寄り道をします。
先ほど記載した、角運動量(L:回転運動の大きさ)は、半径(r)× 運動量(p)(勢い、と解釈して!)です。
そしてこの式を分解すると、運動量(p)(勢い)は、質量(m)✕速度(v)。
さらに、速度(v)は、角速度(回転速度)(w)× 半径(r)に分解されます。
まとめると、こうなります。
そして角運動量保存則に当てはめると、慣性モーメント(回転のしにくさ)は質量(重さ)(m)× 半径(r)の二乗ということになります。
3.まとめ
ここまでの式が出たところで、やっと回転軸の太い・細いの話に戻れます。
先ほど出した、回転のしづらさを表す慣性モーメント(I)は、質量(m)× 半径(r)の二乗。
これをポール上での回転に置き換えたときに、質量(m)は私の体重、半径(r)はポールの回転軸と私の体の距離と考えると、
私(体重)がポールに近づくことで、回転半径が小さくなり
慣性モーメントが小さくなる=回転軸が細くなる=回転が早くなる
逆に、ポールから離れることで、回転半径が大きくなり
慣性モーメントトが大きくなる=回転軸が太くなる=回転が遅くなる
1.のところで数字をあてはめてみたように、慣性モーメントが小さくなることで角速度(回転速度)が上がるというイメージと一致します。
体重は変わらないけれども、ポールとの距離は変えられる。
だから、角速度(回転速度)を上げるには回転軸を細くする必要がある!
となるわけです。
文章でまとめると
物体の回転運動には、角運動量保存の法則がある。
そこで定義されている慣性モーメントっていう「回転のしづらさ(?)」みたいな概念は、定義上、質量に半径の二乗を掛けた積で表す。
そして、質量を体重と置き換えるならば、半径を縮めれば回転速度が上がる、という仕組み。
ということになるのかな。
でも、文章だけだとやっぱり全然わからなかったので、物理学で使われている式を駆使して説明してみました。
理科はホント苦手だったので、解釈の仕方とかイマイチ自信ないけどたぶんこの考え方で合っている・・はず!
回転軸を理解して回転をコントロールできるようになるといろいろな技を組み合わせることができます!
 |
価格:3,885円 |
![]()
 |
ポールダンス用!フィンガーレスグローブ 左右セット/子供/大人/サイズ 価格:3,800円 |
![]()